파이썬 프로그래밍으로 배우는 컴퓨터 비전 - Chapter 1 (3)
1.4 SciPy
이번 시간에는 저번시간에 이어서 1장의 컴퓨터비전의 중요한 파이썬 라이브러리인 SciPy에 대해서 알아보도록 하겠습니다.
SciPy 는 NumPy를 기반으로 하는 수학을 위한 오픈 소스 패키지 입니다. 그리고 수치 통합, 최적화, 통계, 신호 처리, 그리고 우리에게 가장 중요한 이미지 처리등을 포함한 많은 작업에 대한 효율적인 루틴을 제공합니다. 이후 많은 예제를 통해서 SciPy의 많은 유용한 모듈들을 보여드리겠습니다. SciPy는 무료로 이 곳에서 http://scipy.org/Download 다운로드 가능합니다.
이미지 블러링
이미지 컨볼루션의 고전적이고 매우 유용한 예는 이미지의 가우스 블러링 입니다. 본질적으로, (그레이스케일) 이미지 는 블러링 버전인
을 만들기 위해 가우스 커널과 컨볼루션 됩니다. 여기서 *는 컨볼루션을 나타내며
표준 편차
로 정의된 가우스 2D 커널입니다.
가우스 블러링은 보간, 관심 지점 계산 및 더 많은 응용 프로그램에서 작동할 이미지 스케일을 정의하는데 사용됩니다. SciPy는 scipy.ndimage.filters() 라는 필터링 모듈과 함께 이러한 컨볼루션을 계산하는데 빠른 1D 분리 기능을 사용할 수 있습니다. SciPy는 다음과 같은 예시로 사용할 수 있습니다:
from PIL import Image
from numpy import *
from scipy.ndimage import filters
im = array(Image.open('data/empire.jpg').convert('L'))
im2 = filters.gaussian_filter(im,5)
gaussian_filter() 함수의 마지막 매개 변수는 표전 편차입니다.
그림 1-1을 보시면 가 증가함에 따라 이미지의 블러링이 더 강해진다는 것을 볼 수 있습니다. 값이 클수록 자세한 내용은 표시되지 않습니다. 컬러 영상을 블러링하려면, 각 컬러 채널에 가우스 블러링을 적용하기만 하면 됩니다:
from PIL import Image
from numpy import *
from scipy.ndimage import filters
im = array(Image.open('data/empire.jpg'))
im2 = zeros(im.shape)
for i in range(3):
im2[:,:,i] = filters.gaussian_filter(im[:,:,i],5)
im2 = uint8(im2)
마지막 줄의 “unit8”로의 변환이 항상 필요한 것은 아니지만 픽셀 값이 8비트로 표현되도록 강제할 수 있습니다. 변환을 다음과 같이 할 수도 있습니다.
im2 = array(im2, 'unit8')

그림 1-1. scipy.ndimage.filters() 모듈을 사용한 가우스 블러링의 예시. (a) 그레이스케일의 원본 이미지; (b)
이 모듈의 사용과 다양한 매개 변수 선택에 대한 자세한 내용은 http://docs.scipy.org/doc/scipy/reference/ndimage.html 에서 scipy.ndimage의 SciPy의 문서를 참고하시면 됩니다.
이미지 도함수
이미지의 강도가 어떻게 변화하는지는 중요한 정보이며, 이 책에서 볼 수 있듯이 많은 응용 분야에 사용됩니다. 강도 변화는 그레이 레벨 이미지 의 x와 y의 도함수
와
로 설명됩니다. (컬러 이미지의 경우, 일반적으로 각 컬러 채널에 대해 도함수를 취합니다.)
영상 그래디언트는 벡터
로 표현됩니다. 그래디언트는 두 가지 중요한 특성을 가지고 있습니다. 그래디언트의 크기는 아래의 수식으로 설명 가능합니다.
이 수식은 이미지 강도 변화가 얼마나 강한지 설명합니다. 그리고 그래디언트 각도는 아래 수식으로 설명 가능합니다.
이 수식은 이미지의 각 지점(픽셀) 에서 가장 큰 강도 변화의 방향을 나타냅니다. NumPy 함수 arctan2() 는 부호화된 각도를 라디안 단위 로 반환 합니다.
이미지 도함수 계산은 이산 근사치를 사용하여 수행 될 수 있습니다. 이 계산은 아래의 컨볼루션 수식으로 쉽게 구현됩니다.
와
에 대한 두 가지의 일반적인 선택은 Prewitt 필터
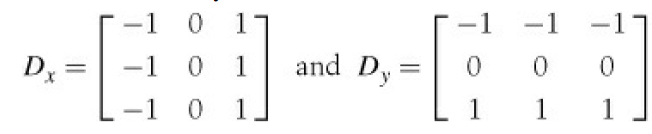 ,
,
그리고 Sobel 필터
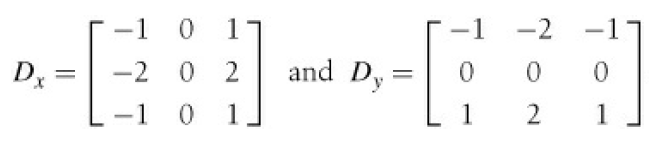 .
.
이러한 도함수 필터는 scipy.ndimage.filters() 모듈의 표준 컨볼루션을 이용해서 쉽게 구현할 수 있습니다. 예시는 다음과 같습니다:
from PIL import Image
from numpy import *
from scipy.ndimage import filters
im = array(Image.open('data/empire.jpg').convert('L'))
# Sobel derivative filters
imx = zeros(im.shape)
filters.sobel(im,1,imx)
imy = zeros(im.shape)
filters.sobel(im,0,imy)
magnitude = sqrt(imx**2+imy**2)
이 예시는 Sobel필터를 사용하여 x와 y의 도함수와 그래디언트 크기를 계산한 것입니다. Sobel 필터의 함수 두 번째 인수는 x 또는 y 도함수를 선택하고, 세번째 인수는 출력을 저장합니다. 그림 1-2 는 Sobel 필터를 사용하여 계산된 도함수가 있는 이미지를 보여줍니다. 두 개의 도함수 이미지에서 양의 도함수는 밝은 픽셀로 표시되고, 음의 도함수는 어두운 색으로 표시됩니다. 회색 영역의 값은 0에 가깝습니다. 이 접근법을 사용하면 이미지 해상도에 의해 결정된 스케일로만 도함수가 취해진다는 단점이 있습니다. 어떤 스케일에서든 이미지 노이즈와 도함수 계산을 더 정확하게 하기 위해서 가우스 도함수 필터를 사용할 수 있습니다 :
여기서 와
는 표준 편차
를 갖는 가우스 함수인
의 x와 y 도함수 값입니다.
이전에 블러링에 사용한 filters.gaussian_filter() 함수는 가우스 도함수로 계산하기 위해 추가 인수를 사용할 수 있습니다. 이미지에서 이 기능을 사용하려면 아래 예시를 참고하시면 됩니다:
sigma = 5 # standard deviation
imx = zeros(im.shape)
filters.gaussian_filter(im, (sigma,sigma), (0,1), imx)
imy = zeros(im.shape)
filters.gaussian_filter(im, (sigma,sigma), (1,0), imy)
세 번째 인수는 두 번째 인수에 의해 결정된 표준 편자를 사용하여 각 방향에서 사용할 도함수의 순서를 지정합니다. 자세한 내용은 설명서 를 참고하십시오. 그림 1-3 은 다양한 스케일의 도함수와 그래디언트의 크기를 보여줍니다. 그림 1-1 의 동일한 스케일에서의 블러링 이미지와 비교해 보십시오.

그림 1-2. Sobel 도함수 필터를 사용하여 이미지 도함수를 계산한 예시: (a) 그레이 스케일의 원본 이미지 ; (b) x-도함수 ; (c) y-도함수 ; (d) 그래디언트 크기

그림 1-3. 가우스 도함수를 사용하여 이미지 도함수를 계산한 예: x-도함수 (위) ; y-도함수 (중간) ; 그래디언트 크기 (아래); (a) 그레이 스케일의 원본 이미지; (b) 가우스 도함수 필터
형태학 - 객체 개수
형태학(Morphology) 는 기본적인 형태를 측정하고 분석하기 위한 체계이자 이미지 처리 방법의 집합입니다. 형태학은 일반적으로 이진 이미지에 적용되지만 그레이스케일과 함께 사용할 수도 있습니다. 이진 이미지는 각 픽셀이 일반적으로 0과 1의 두 값만 취하는 이미지 입니다. 이진 이미지는 예를 들어 물체를 세거나 물체의 크기를 측정하려는 의도로 이미지에 임계값을 적용한 결과인 경우가 많습니다. 형태학의 요약은 다음 위키피디아에 잘 정리되어 있습니다.(http://en.wikipedia.org/wiki/Mathematical_morphology) 형태학전 연산은 scipy.ndimage 의 morphology 모듈 에 저장되어 있습니다. 이진 영상의 계산 및 측정 함수들은 scipy.ndimage 의 measurements 모듈에 저장되어 있습니다. 사용 방법에 대한 간단한 예를 살펴 보겠습니다. 그림 1-4의 이진 이미지를 살펴 보겠습니다. 다음의 예시를 사용하여 해당 이미지의 객체 수를 계산할 수 있습니다:
from PIL import Image
from numpy import *
from scipy.ndimage import measurements,morphology
# load image and threshold to make sure it is binary
im = array(Image.open('data/houses.png').convert('L'))
im = 1*(im<128)
labels, nbr_objects = measurements.label(im)
print("Number of objects:", nbr_objects)
이 예시는 이미지를 불러온 뒤 임계 값을 이용하여 이미지를 이진 값으로 변환 합니다. 1을 곱하면 boolean array가 이진 array로 변환 됩니다. 그런 다음 함수 label() 은 개별 객체를 찾고 해당 객체가 속한 픽셀의 정수 라벨을 할당합니다. 그림 1-4는 라벨 array를 보여줍니다. 그레이스케일의 값은 객체 인덱스를 나타냅니다. 보시다시피, 몇몇 객체들 사이에는 작은 연결들이 있습니다. 다음 예시를 통해 binary_opening() 이라는 연산을 사용하여 연결들은 제거하는 방법을 알게 될 것입니다:
# morphology - opening to separate objects better
im_open = morphology.binary_opening(im,ones((9,5)),iterations=2)
labels_open, nbr_objects_open = measurements.label(im_open)
print("Number of objects:", nbr_objects_open)
binary_opening()의 두 번째 인수는 픽셀을 중심으로 사용할 때 사용할 이웃을 나타내는 array인 구조 요소를 지정합니다. 위의 예시의 경우에는 y 방향으로 9 픽셀 (위로 4 픽셀, 아래로 4픽셀), x 방향으로 5 픽셀을 지정했습니다. 임의의 array 를 구조 요소로 지정할 수 있습니다; 0이 아닌 요소가 인접 요소를 결정합니다. 매개 변수 반복에 따라 연산을 적용할 횟수가 결정됩니다. 이 방법을 사용하여 객체 수가 어떻게 변하는지 확인해 보세요. binary_opening() 을 적용한 이후의 이미지와 해달 라벨 이미지는 그림 1-4에 나와 있습니다. 예상할 수 있듯이, binary_closing()이라는 이름의 함수는 반대의 연산을 수행합니다. 이 함수 뿐만 아니라 morphology 와 measurements 모듈의 다른 함수들은 직접 찾아서 연습해 보시길 추천드립니다. 자세한 설명은 scipy.ndimage 설명서 (http://docs.scipy.org/doc/scipy/reference/ndimage.html) 에서 자세히 확인 할 수 있습니다.

그림 1-4. 형태학의 한 예시. binary _opening() 함수를 통해 객체를 분리한 후 객체의 개수를 계산했습니다. (a) 원본 이진 이미지; (b) 원본에 해당하는 라벨 이미지; (c) binary_opening() 함수를 사용한 후 이진 이미지; (d) binary_opening() 함수를 사용한 이미지의 해당하는 라벨 이미지
유용한 SciPy 모듈들
SciPy 는 입력 및 출력에 유용한 모듈들도 제공합니다. 그 모듈들 중 두 개는 io 와 misc 입니다.
.mat 파일 읽기 및 쓰기
Matlab의 .mat 파일 형식으로 저장된 데이터가 있거나 온라인에서 흥미로운 데이터 세트를 발견한 경우 scipy.io 모듈을 사용하여 이를 읽을 수 있습니다. 방법은 다음과 같습니다:
data = scipy.io.loadmat('test.mat')
객체 데이터는 원래 .mat 파일에 저장된 변수 이름에 해당하는 키 값이 있는 dictionary 를 포함합니다. 변수는 array 형식 입니다. .mat 파일에 저장하는 것도 간단합니다. 저장할 모든 변수가 포함된 dictionary 를 만들고 savemat() 함수를 사용하면 됩니다:
data = {}
data['x'] = x
scipy.io.savemat('test.mat',data)
이 예시는 MatLab에서 array x 를 읽을 때, array x 의 이름이 ‘x’ 가 되게 저장합니다. scipy.io 에 대한 자세한 내용은 온라인 설명서(http://docs.scipy.org/doc/scipy/reference/io.html) 에서 확인 할 수 있습니다.
Array 를 이미지로 저장
array 객체를 사용하여 이미지를 조작하고 계산을 하기 때문에, array 를 직접 이미지 파일로 저장 할 수 있는 것이 유용합니다. 이 책의 많은 이미지들은 바로 이와 같이 만들어 졌습니다. imsave() 함수는 scipy.misc 모듈을 통해 사용 가능합니다. array를 파일에 저장하려면 다음과 같이 사용하시면 됩니다:
from scipy.misc import imsave
imsave('test.jpg',im)
scipy.misc 모듈에는 유명한 “Lena” 테스트 이미지도 포함되어 있습니다.:
lena = scipy.misc.lena()
이 함수는 512x512 의 그레이 스케일 array 이미지 버전을 제공합니다.
이번 시간에는 파이썬 라이브러리 SciPy에 대해서 간단히 소개 하는 시간을 가졌습니다. 다음 포스팅에서는 좀 더 심화 과정인 이미지 노이즈 제거에 대해서 알아보고 1장을 마무리 하도록 하겠습니다.
출처 : Solem, J.E. (no date) Programming Computer Vision with python, Programming Computer Vision with Python. Available at: http://programmingcomputervision.com/ (Accessed: December 7, 2022).
Leave a comment